こんにちは!テツ(@tetsulog2020)です。
FP試験の勉強、おつかれ様です。
私も1年前の今ごろに3級の勉強を始めましたが、テキスト序盤で登場した「6つの係数」を見て眉間に6本のしわを寄せたのをよく覚えています。
・現価係数
・終値係数
・年金現価係数
・年金終値係数
・減債基金係数
・資本回収係数


という感じで毛嫌いしている人も多いかと思いますが、6つの係数問題はコツさえ掴めば簡単に全問正解できる超サービス問題です。
2級の問題も簡単に解けるようになります。
今回は「6つの係数」の超簡単な覚え方を解説します。
もくじ
まずは6つの係数をおさらい

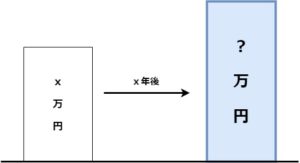
1.終値係数
現在の金額を複利で運用した場合の、x年後の金額を求める
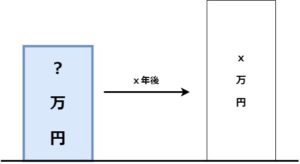
2.現価係数
x年後にx万円に達するために必要な元本を求める
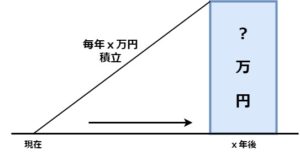
3.年金終値係数
毎年x万円積み立てた場合のx年後の金額を求める
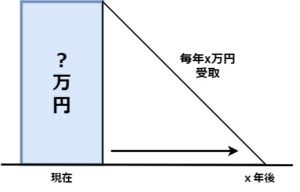
4.年金現価係数
毎年x万円を受け取るために必要な元本を求める
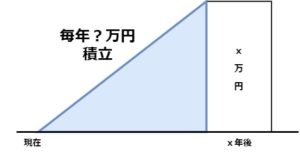
5.減債基金係数
x年後にx万円用意するための毎年の積立額を求める
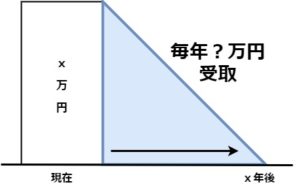
6.資本回収係数
x万円をx年間で取り崩した場合の、毎年の受取額を求める
6つの係数で知りたい金額は大きく3種類
6つの係数問題で問われる金額は必ず以下の3種類のどれかで、どの金額が知りたいかで係数を絞り込めます。
1.必要な元本が知りたい問題
2.n年後の金額が知りたい問題
3.毎年の積立(or受取)額が知りたい問題
ひとつずつ解説します。
1.必要な元本が知りたい問題
例えばこのような問題です。
「年利3%で10年後に100万円用意するには元本はいくら必要か?」
元本を求める係数には「現価」のワードが入ります。
6つの係数の中では「現価係数」か「年金現価係数」に絞ることができます。
2.n年後の金額が知りたい問題
例えばこのような問題です。
「100万円を年利3%で運用した場合の10年後の金額はいくらか?」
n年後の金額を求める係数には「終値」のワードが入ります。
6つの係数の中では「終値係数」か「年金終値係数」に絞ることができます。
3.毎年の積立(or受取)額が知りたい問題
例えばこのような問題です。
「年利3%で10年後に100万円を用意するには毎年いくら積み立てる必要があるか?」
この分類だけ共通のワードがないので少し覚えずらいですが、積立なら「減債基金係数」、受取なら「資本回収係数」になります。
まずはこの法則で分類することで1/6→1/2まで絞れます。
さらにここから一つに絞る方法を次で解説します。
毎年積立(or受取)方式なら「年金」
例えばこのような問題です。
「5年間にわたって毎年10万円ずつ受け取りたい。年利2%の場合、必要な元本はいくらか?」
まず、元本を知りたい問題なので「現価係数」か「年金現価係数」のどちらかです。
さらに、この問題では”毎年10万円ずつ受け取る”=毎年受取方式となるので「年金現価係数」ということが分かります。
「減債基金係数」と「資本回収係数」の覚え方
「減債基金係数」と「資本回収係数」の2つは共通のワードこそありませんが、「基金」と「回収」の意味に着目すればそれぼど難しく考える必要はありません。
・「基金」・・・積立
・「回収」・・・受取
あとは、言葉の意味を覚えてしまえば超簡単です。
減債基金係数の意味
「減債」は債務を減らすことで「基金」はある目的のために積み立てておく資金です。
つまり、債券の発行体が償還のための金額を積み立てているとイメージすれば簡単ですね。
資本回収係数の意味
資本回収係数は住宅ローンなどの借金を銀行側の目線で考えると簡単に理解できます。
銀行は自分たちの資本の一部を消費者へ融資し、利息を加えた額を回収します。
資本を回収するので「資本回収係数」。まんまですね。。
実際の問題で6つの係数を覚えよう

次の例題1&例題2がどの係数を用いるか考えてみましょう。
例題1
年利2%で毎年5万円を20年間積み立てた場合の5年後の金額はいくらか?
例題2
年利2%で5年後に100万円用意するには毎年いくら積み立てる必要があるか?
◆例題1の考え方
✓n年後の金額が知りたい問題なので、「終値係数」か「年金終値係数」
✓毎年積立方式なので「年金」
ということで用いる係数は「年金終値係数」になります。
◆例題2の考え方
✓毎年の積立(or受取)額が知りたい問題なので「減債基金係数」か「資本回収係数」
今回は積立なので用いる係数は「減債基金係数」になります。
これでもうバッチリですね!
まとめ

元本が知りたかったら「現価係数」か「年金現価係数」
n年後の金額が知りたかったら「終値係数」か「年金終値係数」
毎年積立(or受取)方式なら「年金」
毎年の積立額が知りたかったら「減債基金係数」(積立=基金)
毎年の受取額が知りたかったら「資本回収係数」(受取=回収)
最後まで読んでいただき、ありがとうございました!
今後もFP試験受験者に役立つ情報をアップしていきます!






